Category: Algebra

Posted on

Binomische Formeln

Ein Binom ist z.B sowas:
$$(a+b)^2 \text{ oder }(3-6)^2\text{ oder }(x+4)^2$$
entscheidend ist also, man hat zwei Summanden in einer Klammer und quadriert das anschliessend. Also von innen nach außen gelesen.
Binomische Formeln fassen den Vorgang des Ausklammerns der Terme zusammen in eine Formel.

Wie viele Binomische Formeln gibt es?
Es gibt drei Stück, weil wir drei Möglichkeiten haben wie wir $+$ oder $\color{red}-$ in den Klammern finden können: $$(+)(+)\text{, }(\color{red}-)(\color{red}-)\text{ oder }(+)(\color{red}-)$$

Wegen $(+)(\color{red}-)=(\color{red}-)(+)$ haben wir also mit den genannten 3 alle Möglichkeiten

1. Binomische Formel:
$$
\begin{align*}
(a+b)^2 &=(a+b)\cdot (a+b) \\
&= a\cdot a + a\cdot b + b\cdot a + b^2\\
&= a^2 + ab + ab + b^2\\
&= \underline{\underline{a^2+2ab+b^2}}\\
&= b^2+2ba+a^2\\
&=(b+a)^2
\end{align*}
$$
2. Binomische Formel:
$$
\begin{align*}
(a\color{red}-b)^2 &=(a\color{red}-b)\cdot (a\color{red}-b)\\
&= a\cdot a \color{red}- a\cdot b \color{red}- b\cdot a + b^2\\
&= a^2 \color{red}- ab \color{red}- ab + b^2\\
&=\underline{\underline{a^2\color{red}-2ab+b^2}}\\
&= b^2\color{red}-2ba+a^2\\
&=(b\color{red}-a)^2
\end{align*}
$$
3. Binomische Formel:
$$
\begin{align*}
(a+b)\cdot (a\color{red}-b) &= a\cdot a + a\cdot b \color{red}- b\cdot a + b\cdot b\\
&= a^2 + \underbrace{(ab \color{red}- ab)}_{=0} + b^2\\
&= \underline{\underline{a^2\color{red}-b^2}}
\end{align*}
$$

Trick mit 3. Binom und Parabel-Nullstellen

parabel-scheitelpkt
Parabel Nullstellen heißt, wir müssen die quadratische Funktionsgleichung nach $x$ auflösen.
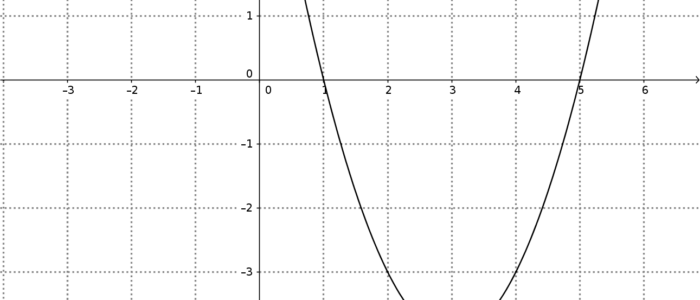
Das Tolle ist, wenn wir jetzt wissen wollen was für Nullstellen eine Parabel hat, also was die Lösung einer quadratischen Gleichung nach $x$ ist oder nochmal anders gesagt, was die Schnittpunkte des Funktionsgraphen von $f$ mit der $x$-Achse sind, dann können wir das besonders schnell, wenn die die Funnktionsgleichung von $f$ die Form einer 3. Binomischen Formel hat z.B. hier
$$
f(x)=x^2-16
$$
dann sehen wir: vorne steht ein $x^2$ das könnte das $a^2$ aus der 3. Binomischen Formel sein und die $16$ könnte (weil es eine einfache Quadratzahl $16$ ist, können wir die Wurzel $\sqrt{16}=4$ daraus im Kopf rechnen und sie ist $4$ – klar!) als $4^2$ ein $b^2$ sein. Dann ist die Gleichung zwar sowieso schon “einfach” (meint ohne mühsame pq-Formel) nach $x$ aufzulösen:
$$
\begin{align*}
f(x)&=0\\
x^2-16&=0 & &|+16\\
x^2 &= 16 & &| \sqrt{\cdot}\\
x_{1,2} &= \pm\sqrt{16}\\
x_{1,2} &= \pm 4\\
\\
\Rightarrow \color{orange}{x_1}&=-4\\
\color{orange}{x_2}&=4
\end{align*}
$$
aber noch schneller geht es mit der Überlegung, dass ja dann die Funktion sich wegen 3. Binomischer Formel schreiben lässt als
$$
f(x)=x^2-16=(x+4)(x-4)
$$

Jetzt DER TRICK:

da ein Produkt, hier das $(x+4)$ “mal” $(x-4)$, immer Null sein muss, wenn einer der Faktoren also entweder $(x+4)$ oder $(x-4)$ Null ist, sieht man sofort die Lösungen: nämlich die Zahlen in den Klammern mit jeweils umgekehrtem Vorzeichen:
$$
\begin{align*}
f(x)&=0\\
(x+4)(x-4)&=0\\
\Rightarrow x+4 &=0 \text{ oder }x-4=0\\
\Rightarrow \color{orange}{x_1}&=-4\\
\color{orange}{x_2}&=4\\
\end{align*}
$$
Also hätte man die Nullstellen $\color{orange}{x_1}$ und $\color{orange}{x_2}$ direkt ablesen können, indem man sich das für $x$ in die Klammern denkt, was die jeweilige Klammer Null setzen würde:
$$
\begin{align*}
(\color{orange}{x_1}+4)(\color{orange}{x_2}-4)&=0\\
\underbrace{(\color{orange}{-4}+4)}_{=0}\underbrace{(\color{orange}{4}-4)}_{=0}&=0\\
\end{align*}
$$

Das gleiche geht natürlich bei allen quadratischen Funktionen die wie ein 3. Binom aussehen z.B.

$$
\begin{align*}
f(x)&=x^2 – 9 = (x+3)(x-3)\\
\Rightarrow \color{orange}{x_1}&=-3 \text{ und }\color{orange}{x_2}=3\\
\\
f(x)&=x^2 – 25 = (x+5)(x-5)\\
\Rightarrow \color{orange}{x_1}&=-5 \text{ und }\color{orange}{x_2}=5\\
\\
f(x)&=x^2 – 4 = (x+2)(x-2)\\
\Rightarrow \color{orange}{x_1}&=-2 \text{ und }\color{orange}{x_2}=2\\
\\
f(x)&=x^2 – 144 = (x+12)(x-12)\\
\Rightarrow \color{orange}{x_1}&=-12 \text{ und }\color{orange}{x_2}=12\\
\end{align*}
$$
usw.

Aber Vorsicht, wenn sowas wie $x^2\color{red}+ 9$ da steht, dann gilt das alles nicht!!
$$
\begin{align*}
f(x)&=x^2 + 9 \color{red}\neq (x+3)(x-3)\\
\end{align*}
$$
und die dazugehörige Parabel hätte $\color{red}{\text{KEINE}}$ Nullstelle:

$$
\begin{align*}
f(x)&=0\\
x^2 + 9 &=0 &|-9\\
x^2 &= -9 &|\sqrt{\cdot}\\
x &=\pm \sqrt{\color{red}{-9}} &\text{ ist Verboten!!}\\
\Rightarrow \text{keine Lösung!}
\end{align*}
$$

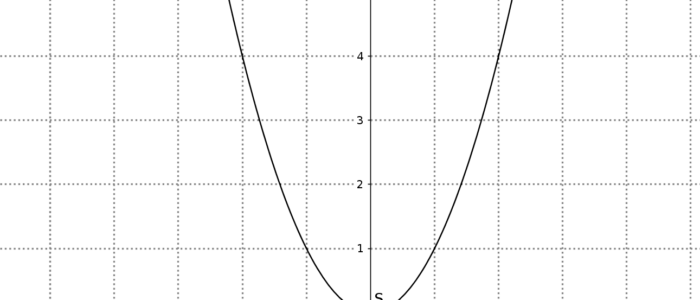
Ist ja auch Logisch, denn $f(x)=x^2+9$ ist die Scheitelpunktform und man kann den Scheitelpunkt $S(0|9)$ direkt ablesen. Das heißt also der $y$-Wert liegt ÜBER der $x$-Achse und die Parabel ist nach oben geöffnet (kann man daran sehen, dass vor dem $x^2$ kein “$-$” steht)

normalparabel-scheitelpkt-ohne-nullstellen

Also schneidet sie die $x$-Achse nicht und hat damit auch keine Nullstellen 🙂

    Nachhilfe Anfrage senden:

          


    Ich habe die  Datenschutzerklärung zur Kenntnis genommen. Ich stimme zu, dass meine Angaben und Daten zur Beantwortung meiner Anfrage elektronisch erhoben und gespeichert werden.

    Posted on

    Die pq-Formel

    Die $\color{blue}p$-$\color{green}q$-Formel ist eine Lösungsformel für quadratische Gleichungen mit $\color{red}{\text{einfachem quadratischen Teil}}$ (nichts steht vor dem $x^2$ bzw. nur eine gedachte $\color{red}1$), $p$-fachem $\color{blue}{\text{linearen Teil}} und einer $\color{green}{\text{Konstanten}} $\color{green}q$. Die quadratsche Gleichung muss also in Normalform vorliegen:
    $$\text{wenn}f(x)=\color{red}1\cdot x^2 + \color{blue}{p}x + \color{green}{q}\text{,}$$
    dann sind die Nullstellen $\color{orange}{x_1}$ und $\color{orange}{x_2}$ von $f(x)$ gegeben durch
    $$\color{orange}{x_{1,2}} = \text{ }- \frac{\color{blue}{p}}{2}\pm\sqrt{\left(\frac{\color{blue}{p}}{2}\right)^2-\color{green}{q}}$$
    Man möchte also Nullstellen (Schnittpunkte der Funktion $f$ mit der $x$-Achse) finden bzw. Lösungen für die Gleichung $$f(x)=0$$

    Wie kommt man auf die p-q-Formel?

    Wenn man die Nullstellen der Normalform einer Parabel berechnet, dann kommt man automatisch auf die $\color{blue}p$-$\color{green}q$-Formel
    Wir setzen die Normalform der Gleichung mal ein und versuchen die Gleichung mit allen Techniken die wir bis jetzt kennen nach $x$ aufzulösen:

    $$\begin{align*}
    x^2 + \color{blue}{p}x + \color{green}{q} &= 0 & &| \text{quadr. ergänzen}\\
    &\\
    x^2 + \color{blue}{p}x + \underbrace{\left(\frac{\color{blue}{p}}{2}\right)^2 -\left(\frac{\color{blue}{p}}{2}\right)^2}_{=0} + \color{green}{q} &= 0 & &| \text{nicht verändert}\\
    \underbrace{x^2 + \color{blue}{p}x + \left(\frac{\color{blue}{p}}{2}\right)^2}_{} -\left(\frac{\color{blue}{p}}{2}\right)^2 + \color{green}{q} &= 0 & &| \text{1. Binom}\\
    \underbrace{\left(x+ \frac{\color{blue}{p}}{2}\right)^2 + \color{green}{q} -\left(\frac{\color{blue}{p}}{2}\right)^2}_{\color{cyan}{\text{Scheitelpunkt-Form ;)}}} &= 0 & &| -\color{green}{q} +\left(\frac{\color{blue}{p}}{2}\right)^2\\
    \left(x+ \frac{\color{blue}{p}}{2}\right)^2 &= \left(\frac{\color{blue}{p}}{2}\right)^2-\color{green}{q} & &| \sqrt{\cdot}\\
    x+ \frac{\color{blue}{p}}{2} &= \pm\sqrt{\left(\frac{\color{blue}{p}}{2}\right)^2-\color{green}{q}} & &| – \frac{\color{blue}{p}}{2}\\
    &\\
    \color{orange}{x_{1,2}} &= \text{ }- \frac{\color{blue}{p}}{2}\pm\sqrt{\left(\frac{\color{blue}{p}}{2}\right)^2-\color{green}{q}} & &| \text{fertig..}
    \end{align*}
    $$

      Nachhilfe Anfrage senden:

            


      Ich habe die  Datenschutzerklärung zur Kenntnis genommen. Ich stimme zu, dass meine Angaben und Daten zur Beantwortung meiner Anfrage elektronisch erhoben und gespeichert werden.

      Posted on

      Quadratische Gleichungen und Parabeln

      Eine Quadratische Funktion ist eine, die als höchsten Exponenten $2$ hat. Das heißt, dass sich die Funktionswerte $f(x)=y$ im Verhältnis zum Eingabewert (meistens $x$) quadratisch verhalten. Der Artikel hier hat zu tun mit dem Lösen von quadratische Gleichungen bzw. dem finden von Nullstellen von solchen Parabeln.

      Für diese Art von Funktion kennen wir verschiedene Formen der Funktionsgleichung. Wir schauen uns hier an, welche Formen entstehen können und was wir aus den unterschiedlichen Formen alles besonders gut raus lesen können.

      Allgemeine Form

      $$f(x)=\color{red}a x^2 + \color{blue}{b}x + \color{green}{c}$$
      hier haben wir eine Struktur in der wir dem $\color{red}{\text{quadratischen Teil}}$ ($\color{red}{x^2}$), dem $\color{blue}{\text{linearen Teil}}$ ($\color{blue}{x^1}$) und dem $\color{green}{\text{konstanten Teil}}$ ($\color{green}{x^0}$) jeweils einen Koeffizienten ($a$, $b$ und $c$) zuweisen. Und zwar so:

      $$
      \begin{align*}
      f(x)&=\color{red}{a}\cdot x^2 + \color{blue}{b}\cdot x^1 + \color{green}{c}\cdot x^0 \\
      &=\color{red}{a}x^2 + \color{blue}{b}x + \color{green}{c} & &
      \end{align*}
      $$

      Man mache sich die Struktur der Gleichung klar! die Reihenfolge der Summanden und der Koeffizienten spielt keine Rolle, da wir irgendwann gelernt haben, dass man Summanden in einer Summe immer beliebig vertauschen darf und auch Faktoren in einem Produkt. Ob wir also schreiben $$f(x)=x^0\cdot c + a\cdot x^2 + x^1\cdot b$$ oder die Form oben, ist egal.

      Übrigens: Was aber NICHT geht, ist die Koeffizienten vor andere Teile zu schreiben (z.B. $b\cdot x^2$ statt $a\cdot x^2$. Wenn man sich einmal für Koeffizienten Namen entschieden hat muss man sie auch dem jeweiligen Teil der Funktion zugeordnet lassen. Das ist das einzig wichtige! Welche Buchstaben man für die Koeffizienten nimmt ist wiederum völlig egal. Man kann sie auch $a_1$, $a_2$ und $a_3$ nennen oder $a$, $p$ und $q$.

      $$f(x)=\color{red}a x^2 + \color{blue}{b}x + \color{green}{c}$$

      Normalform

      $$f(x)=x^2 + \color{blue}{p}x + \color{green}{q}$$
      Bei der Normalform ist einfach der Keaffizient vor dem $\color{red}{\text{quadratischen Teil}}$ eins. Also die Funktion hat vor dem $x^2$ nichts mehr stehen.
      $$f(x)=x^2 + \color{blue}{p}x + \color{green}{q}$$

      Scheitelpunktform

      $$ f(x)= \left( x + \underbrace{\frac{\color{blue}p}{2}}_{\substack{-\color{cyan}{x_s}}} \right)^2 + \underbrace{\color{green}q-\left(\frac{\color{blue}p}{2}\right)^2}_{\substack{\color{cyan}{y_s}}}$$
      Der Scheitelpunkt $S$ ist dann $$S(\color{cyan}{x_s}|\color{cyan}{y_s})$$

      Wir haben hier also ein Binom und eine Konstante

      $$f(x)=\left(x+\frac{\color{blue}p}{2}\right)^2+\color{green}q-\left(\frac{\color{blue}p}{2}\right)^2$$

      Nullstellenform oder Linearfaktorzerlegung

      $$f(x)= \color{red}a(x-\color{orange}{x_1})(x-\color{orange}{x_2})$$
      $\color{red}a$ ist der Faktor vor dem $x^2$ wenn man die Klammern ausklammern würde und diese Form in die allgemeine Form bringt. Die beiden orangenen Werte sind genau die Nullstellen $\color{orange}{x_1}$ und $\color{orange}{x_2}$
      $$f(x)= \color{red}a\left(x-\color{orange}{x_1})(x-\color{orange}{x_2}\right)$$

      Beispiele für verschiedene Formen

      Fangen wir mit der denkbar einfachsten quadratischen Funktion an und zeigen der Reihe nach an
      $$
      \begin{align*}
      f(x)&=\text{allgemeine Form}\\
      &=\text{Normal-Form}\\
      &=\text{Scheitelpunkt-Form}\\
      &=\text{Nullstellen-Form}\\
      \end{align*}
      $$
      Ein und dieselbe Parabel hat zwar einen Graphen aber viele Darstellungen in der Funktionsgleichung. Ist klar, da man ja durch Thermumformungen alles mögliche machen kann mit der Funktion ohne das “wie sie funktioniert” zu verändern.
      $$
      \begin{align*}
      f(x)&=x^2\\
      &=x^2\\
      &=x^2\\
      &=x\cdot x
      \end{align*}
      $$

      normalparabel

      Wie nennt man die? Das ist eine Normalparabel. Warum? Normal bedeutet hier, dass vor dem $x^2$ kein Koeffizient (außer $1$, da $x^2=\color{red}1\cdot x^2$) bzw. der quadratische Teil der Funktion “normiert” (also eins) ist. In der allgemeinen Form wäre der Koeffizient dazu $\color{red}{a=1}$, $\color{blue}{b=0}$ und $\color{green}{c=0}$

      Was ist mit dieser Funktion:

      normalparabel-3r-4u

      Sie hat den Scheitelpunkt wie man dem Graphen von $f$ ablesen kann bei $S(3|-4)$ und die Nullstellen bei $x_1=1$ und $x_2=5$
      $$
      \begin{align*}
      f(x)&=x^2-6x+5\\
      &=x^2-6x+5\\
      &=(x-3)^2-4\\
      &=(x-1)(x-4)
      \end{align*}
      $$
      Also ist $\color{red}{a=1}$, $\color{blue}{b=6}$ bzw. in der Normal-Form $\color{blue}{p=6}$ und $\color{green}{c=5}$ was in der Normal-Form $\color{green}{q=5}$ entspricht.

      Hier ist noch ein Link zum interaktiven Verständniss mit GeoGebra: Parabel verstehen

        Nachhilfe Anfrage senden:

              


        Ich habe die  Datenschutzerklärung zur Kenntnis genommen. Ich stimme zu, dass meine Angaben und Daten zur Beantwortung meiner Anfrage elektronisch erhoben und gespeichert werden.