Eine Quadratische Funktion ist eine, die als höchsten Exponenten $2$ hat. Das heißt, dass sich die Funktionswerte $f(x)=y$ im Verhältnis zum Eingabewert (meistens $x$) quadratisch verhalten. Der Artikel hier hat zu tun mit dem Lösen von quadratische Gleichungen bzw. dem finden von Nullstellen von solchen Parabeln.
Für diese Art von Funktion kennen wir verschiedene Formen der Funktionsgleichung. Wir schauen uns hier an, welche Formen entstehen können und was wir aus den unterschiedlichen Formen alles besonders gut raus lesen können.
Allgemeine Form
$$f(x)=\color{red}a x^2 + \color{blue}{b}x + \color{green}{c}$$
hier haben wir eine Struktur in der wir dem $\color{red}{\text{quadratischen Teil}}$ ($\color{red}{x^2}$), dem $\color{blue}{\text{linearen Teil}}$ ($\color{blue}{x^1}$) und dem $\color{green}{\text{konstanten Teil}}$ ($\color{green}{x^0}$) jeweils einen Koeffizienten ($a$, $b$ und $c$) zuweisen. Und zwar so:
$$
\begin{align*}
f(x)&=\color{red}{a}\cdot x^2 + \color{blue}{b}\cdot x^1 + \color{green}{c}\cdot x^0 \\
&=\color{red}{a}x^2 + \color{blue}{b}x + \color{green}{c} & &
\end{align*}
$$
Man mache sich die Struktur der Gleichung klar! die Reihenfolge der Summanden und der Koeffizienten spielt keine Rolle, da wir irgendwann gelernt haben, dass man Summanden in einer Summe immer beliebig vertauschen darf und auch Faktoren in einem Produkt. Ob wir also schreiben $$f(x)=x^0\cdot c + a\cdot x^2 + x^1\cdot b$$ oder die Form oben, ist egal.
Übrigens: Was aber NICHT geht, ist die Koeffizienten vor andere Teile zu schreiben (z.B. $b\cdot x^2$ statt $a\cdot x^2$. Wenn man sich einmal für Koeffizienten Namen entschieden hat muss man sie auch dem jeweiligen Teil der Funktion zugeordnet lassen. Das ist das einzig wichtige! Welche Buchstaben man für die Koeffizienten nimmt ist wiederum völlig egal. Man kann sie auch $a_1$, $a_2$ und $a_3$ nennen oder $a$, $p$ und $q$.
$$f(x)=\color{red}a x^2 + \color{blue}{b}x + \color{green}{c}$$
Normalform
$$f(x)=x^2 + \color{blue}{p}x + \color{green}{q}$$
Bei der Normalform ist einfach der Keaffizient vor dem $\color{red}{\text{quadratischen Teil}}$ eins. Also die Funktion hat vor dem $x^2$ nichts mehr stehen.
$$f(x)=x^2 + \color{blue}{p}x + \color{green}{q}$$
Scheitelpunktform
$$ f(x)= \left( x + \underbrace{\frac{\color{blue}p}{2}}_{\substack{-\color{cyan}{x_s}}} \right)^2 + \underbrace{\color{green}q-\left(\frac{\color{blue}p}{2}\right)^2}_{\substack{\color{cyan}{y_s}}}$$
Der Scheitelpunkt $S$ ist dann $$S(\color{cyan}{x_s}|\color{cyan}{y_s})$$
Wir haben hier also ein Binom und eine Konstante
$$f(x)=\left(x+\frac{\color{blue}p}{2}\right)^2+\color{green}q-\left(\frac{\color{blue}p}{2}\right)^2$$
Nullstellenform oder Linearfaktorzerlegung
$$f(x)= \color{red}a(x-\color{orange}{x_1})(x-\color{orange}{x_2})$$
$\color{red}a$ ist der Faktor vor dem $x^2$ wenn man die Klammern ausklammern würde und diese Form in die allgemeine Form bringt. Die beiden orangenen Werte sind genau die Nullstellen $\color{orange}{x_1}$ und $\color{orange}{x_2}$
$$f(x)= \color{red}a\left(x-\color{orange}{x_1})(x-\color{orange}{x_2}\right)$$
Beispiele für verschiedene Formen
Fangen wir mit der denkbar einfachsten quadratischen Funktion an und zeigen der Reihe nach an
$$
\begin{align*}
f(x)&=\text{allgemeine Form}\\
&=\text{Normal-Form}\\
&=\text{Scheitelpunkt-Form}\\
&=\text{Nullstellen-Form}\\
\end{align*}
$$
Ein und dieselbe
Parabel hat zwar einen Graphen aber viele Darstellungen in der Funktionsgleichung. Ist klar, da man ja durch Thermumformungen alles mögliche machen kann mit der Funktion ohne das “wie sie funktioniert” zu verändern.
$$
\begin{align*}
f(x)&=x^2\\
&=x^2\\
&=x^2\\
&=x\cdot x
\end{align*}
$$
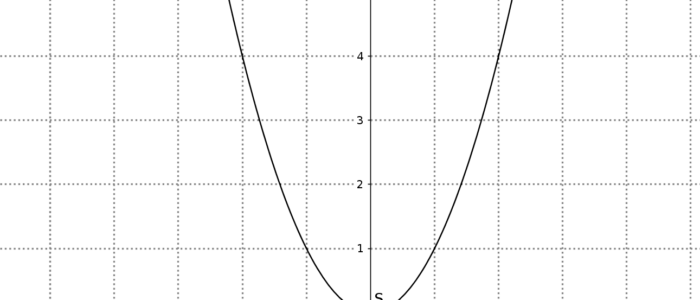
Wie nennt man die? Das ist eine Normalparabel. Warum? Normal bedeutet hier, dass vor dem $x^2$ kein Koeffizient (außer $1$, da $x^2=\color{red}1\cdot x^2$) bzw. der quadratische Teil der Funktion “normiert” (also eins) ist. In der allgemeinen Form wäre der Koeffizient dazu $\color{red}{a=1}$, $\color{blue}{b=0}$ und $\color{green}{c=0}$
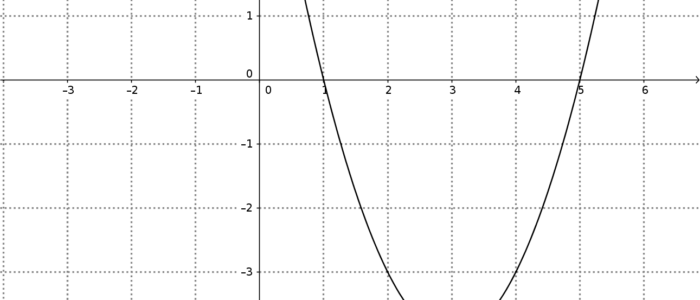
Was ist mit dieser Funktion:

Sie hat den Scheitelpunkt wie man dem Graphen von $f$ ablesen kann bei $S(3|-4)$ und die Nullstellen bei $x_1=1$ und $x_2=5$
$$
\begin{align*}
f(x)&=x^2-6x+5\\
&=x^2-6x+5\\
&=(x-3)^2-4\\
&=(x-1)(x-4)
\end{align*}
$$
Also ist $\color{red}{a=1}$, $\color{blue}{b=6}$ bzw. in der Normal-Form $\color{blue}{p=6}$ und $\color{green}{c=5}$ was in der Normal-Form $\color{green}{q=5}$ entspricht.
Hier ist noch ein Link zum interaktiven Verständniss mit GeoGebra: Parabel verstehen