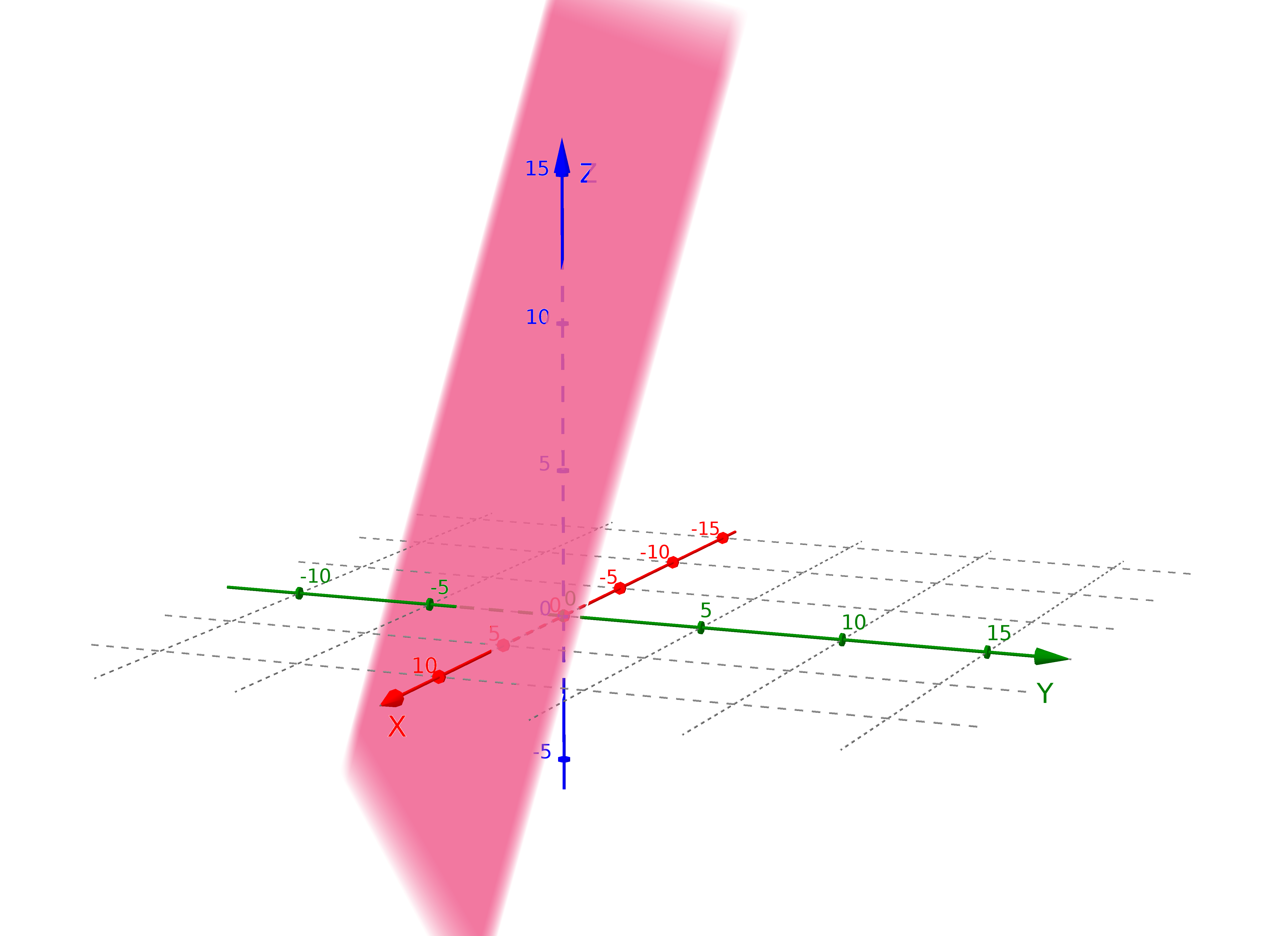
Ebenen im Raum können durch eine Koordinatengleichung beschrieben werden.
Wie viele Koordinaten sind das im Raum? Richtig: 3 Stück. Meistens heißen die x,y und z so wie die Achsen im Koordinatensystem.
Wenn man jetzt z.B. eine Gleichung wie diese aufstellt:
$$\color{violet}{E: \text{ }2x-3y+z=12}$$ dann ist damit eine Ebene $\color{violet}E$ definiert. Man kann auch sagen, alle Punkte im Raum, deren Koordinaten die Gleichung erfüllen bilden die Ebene.
Die Frage ist jetzt natürlich: Wie – Wo ist die Ebene und wie kann man sich davon eine Skizze machen?!
Der Trick ist: Man stellt sich einfach vor die Ebene würde von den Koordinaten-Achsen aufgespießt werden. Das heißt man schaut was die Koordinatengleichung mit nur einer Koordinate ergibt, wenn man die anderen Null setzt:
-
Schnitt mit der $ \color{red}x$-Achse:
Wir fragen uns: an welchem Punkt durchstößt die $\color{red}x$-Achse die Ebene? Wir ignorieren $y$ und $z$ in der Koordinatengleichung und schauen was dann übrig bleibt:
$$E: \text{ }2 \color{red}x\color{gray}{-0y+0z}=12\\
\Rightarrow 2\color{red}x=12\Rightarrow \color{red}{x=6}$$
Also schneidet die $ \color{red}x$-Achse die Ebene $\color{violet}E$ im Punkt $A(\color{red}6|0|0)$.
Genauso für die anderen Achsen:
-
Schnitt mit der $\color{green}y$-Achse:
$$E: \text{ }\color{gray}{0x}-3y\color{gray}{+0z}=12\\
\Rightarrow -3\color{green}y=12\Rightarrow \color{green}{y=-4}$$
Also schneidet die $\color{green}y$-Achse die Ebene $\color{violet}E$ im Punkt $B(0|\color{green}-4|0)$.
-
Schnitt mit der $\color{blue}z$-Achse:
$$E: \text{ }\color{gray}{0x-0y+}\color{blue}z=12\\
\Rightarrow \color{blue}{z=12}$$
Also schneidet die $\color{blue}z$-Achse die Ebene $\color{violet}E$ im Punkt $C(0|0|\color{blue}{12})$.
TIPP: Umgekehrt ist es allgemein nicht so einfach aus der 3-Punkte-Form in die Koordinatenform umzurechnen. Aber man sollte sich merken: wenn die 3 Punkte, mit denen man die Ebene definieren möchte, gerade irgendwelche Punkte auf den 3 Koordinatenachsen sind (das sind all die mit jeweils 2 Null-Koordinaten z.B (0|3|0) oder (15|0|0) usw.), dann wäre es relativ einfach, den Vorgang an dem Beispiel oben rückwärts zu durchlaufen:
Wir tun nun so als hätten wir also die 3 Punkte gegeben: $A(6|0|0)$, $B(0|-4|0)$ und C(0|0|12).
Unser Ansatz ist jetzt
$$a\cdot x + b\cdot y +c\cdot z = 1$$
Fangen wir nicht mit der $z$-Komponente an, da wir einen anderen Rechenvorgang haben wollen wie oben. Fangen wir mit dem $a$ vor dem $x$ an und halten die anderen ($b$ und $c$) noch zu, indem wir sie null setzen. Sprich, wir setzen ein: $x=6$, $b=0$ und $c=0$
$$a\cdot 6 + 0\cdot y +0\cdot z = 1$$ und stellen nach $a$ um:
$$a=\frac{1}{6}$$
also haben wir
$$\frac{1}{6}\cdot x + b\cdot y +c\cdot z = 1$$
und machen dann das Gleiche mit $b$ und $y=-4$
$$0\cdot x + b\cdot (-4) + 0\cdot z = 1 \\
\Leftrightarrow b=-\frac{1}{4}$$
also ist die Gleichung jetzt
$$\frac{1}{6}x–\frac{1}{4}y+c\cdot z = 1$$
und zuletzt noch mit $c$ und $z=12$
$$0\cdot x + 0 \cdot y + c \cdot 12 = 1 \\
\Leftrightarrow c = \frac{1}{12}$$
Die Ebene ist jetzt fertig definiert durch die Gleichung:
$$\frac{1}{6}x–\frac{1}{4}y+\frac{1}{12}z = 1$$
damit wir nicht mit Brüchen rechnen müssen multiplizieren wir die ganze Gleichung jetzt mit dem kleinsten gemeinsamen Vielfachen (kgV) aller Nenner, also $12$ (mache dir klar, dass wir die Gleichung bzw. die durch sie definierte Ebene damit nicht verändern!!)
$$\frac{1}{6}x–\frac{1}{4}y+\frac{1}{12}z = 1\text{ }|\cdot 12$$
$$\frac{12}{6}x–\frac{12}{4}y+\frac{12}{12}z = 12$$
$$2x–3y+z = 12$$